Geometric deep learning is a branch of machine learning that develops algorithms for processing data with inherent geometric structures. Unlike traditional Deep Learning methods like convolutional neural networks (CNNs) and recurrent neural networks (RNNs), which are designed for Euclidean data in flat, continuous spaces, geometric deep learning focuses on non-Euclidean data such as 3D shapes, graphs, and networks. The primary challenge in geometric deep learning is creating models that effectively capture and utilize the intrinsic geometric properties of data.
This requires specialized mathematical tools and techniques from differential geometry, graph theory, and topology. Additionally, geometric deep learning often deals with irregular and unstructured data, necessitating the development of new algorithms and architectures. Geometric deep learning has the potential to significantly advance machine learning by enabling the processing and analysis of non-Euclidean data.
By leveraging intrinsic geometric properties, these algorithms can achieve superior performance in tasks like 3D shape recognition, graph analysis, and network modeling. The field combines traditional deep learning methods with specialized mathematical concepts related to geometry and topology. As geometric deep learning continues to evolve, it is expected to play an increasingly important role in various applications, including computer vision, robotics, natural language processing, and speech recognition.
The development of effective geometric deep learning algorithms requires a comprehensive understanding of both traditional deep learning methods and advanced mathematical concepts in geometry and topology.
Key Takeaways
- Geometric deep learning focuses on developing machine learning models that can effectively handle non-Euclidean data such as graphs, networks, and manifolds.
- Geometric deep learning has applications in AI for tasks such as 3D object recognition, molecular structure analysis, and social network analysis.
- In computer vision, geometric deep learning plays a crucial role in tasks like 3D shape recognition, point cloud analysis, and image registration.
- Geometric deep learning is essential in robotics and autonomous systems for tasks like robot localization, mapping, and navigation in complex environments.
- Challenges in geometric deep learning include developing scalable models, handling noisy and incomplete data, and integrating geometric and non-geometric information. The future directions involve exploring new architectures, improving interpretability, and addressing ethical considerations.
Applications of Geometric Deep Learning in AI
Geometric deep learning has a wide range of applications in artificial intelligence (AI), spanning across various domains such as computer vision, robotics, natural language processing, and speech recognition. In computer vision, geometric deep learning has been used to develop algorithms for 3D shape recognition, object detection, and scene understanding. By leveraging the intrinsic geometric properties of 3D shapes, geometric deep learning algorithms can achieve superior performance in tasks such as shape classification and segmentation.
In robotics, geometric deep learning has been applied to tasks such as robot perception, motion planning, and manipulation. By effectively processing and analyzing non-Euclidean data, geometric deep learning algorithms can enable robots to perceive and interact with their environment more effectively. In natural language processing and speech recognition, geometric deep learning has been used to develop algorithms for tasks such as semantic parsing, sentiment analysis, and speech recognition.
By representing language as a structured graph or network, geometric deep learning algorithms can capture the inherent relationships between words and phrases, leading to more accurate and robust language processing models. Overall, the applications of geometric deep learning in AI are diverse and far-reaching, with the potential to revolutionize the way we develop algorithms for processing and analyzing non-Euclidean data.
The Role of Geometric Deep Learning in Computer Vision
Geometric deep learning plays a crucial role in computer vision by enabling the development of algorithms capable of effectively processing and analyzing non-Euclidean data such as 3D shapes and point clouds. Traditional deep learning methods, such as convolutional neural networks (CNNs), are designed to handle Euclidean data represented in a grid-like structure. However, many real-world datasets in computer vision have an inherent geometric structure that cannot be effectively represented using traditional Euclidean methods.
Geometric deep learning addresses this limitation by developing algorithms that can effectively capture and leverage the intrinsic geometric properties of the data. One of the key applications of geometric deep learning in computer vision is 3D shape recognition. By representing 3D shapes as graphs or point clouds, geometric deep learning algorithms can capture the local and global geometric features of the shapes, leading to more accurate and robust shape recognition models.
Additionally, geometric deep learning has been used for tasks such as object detection and scene understanding, where the input data has a non-Euclidean structure. Overall, the role of geometric deep learning in computer vision is to enable the development of algorithms capable of effectively processing and analyzing non-Euclidean data, leading to superior performance in tasks such as 3D shape recognition, object detection, and scene understanding.
Geometric Deep Learning in Robotics and Autonomous Systems
| Metrics | Value |
|---|---|
| Accuracy | 85% |
| Precision | 90% |
| Recall | 80% |
| F1 Score | 87% |
Geometric deep learning plays a critical role in robotics and autonomous systems by enabling the development of algorithms capable of effectively processing and analyzing non-Euclidean data such as point clouds and sensor data. In robotics, traditional methods for perception and motion planning often struggle to handle the inherent geometric structure of the environment. Geometric deep learning addresses this limitation by developing algorithms that can effectively capture and leverage the intrinsic geometric properties of the data.
One of the key applications of geometric deep learning in robotics is robot perception. By leveraging the intrinsic geometric properties of sensor data such as point clouds, geometric deep learning algorithms can enable robots to perceive their environment more effectively, leading to more accurate and robust perception models. Additionally, geometric deep learning has been used for tasks such as motion planning and manipulation, where the input data has a non-Euclidean structure.
Overall, the role of geometric deep learning in robotics is to enable the development of algorithms capable of effectively processing and analyzing non-Euclidean data, leading to superior performance in tasks such as robot perception, motion planning, and manipulation.
Challenges and Future Directions in Geometric Deep Learning
Despite its potential, geometric deep learning faces several challenges that need to be addressed for its widespread adoption and advancement. One of the key challenges is the development of scalable algorithms capable of handling large-scale non-Euclidean data. Many real-world datasets in applications such as computer vision, robotics, and natural language processing are high-dimensional and complex, requiring the development of efficient algorithms that can process and analyze such data effectively.
Another challenge is the interpretability of geometric deep learning models. As geometric deep learning algorithms become more complex and sophisticated, understanding how they make decisions becomes increasingly important for their practical deployment. Developing methods for interpreting and explaining the decisions made by geometric deep learning models is crucial for their adoption in real-world applications.
In terms of future directions, there is a growing interest in developing hybrid models that combine traditional Euclidean methods with geometric deep learning techniques. By leveraging the strengths of both approaches, hybrid models have the potential to achieve superior performance in a wide range of applications. Additionally, there is a need for further research into developing specialized hardware architectures optimized for geometric deep learning tasks.
As the field continues to evolve, addressing these challenges and exploring new directions will be crucial for advancing the state-of-the-art in geometric deep learning.
Leveraging Geometric Deep Learning for Graph and Network Data
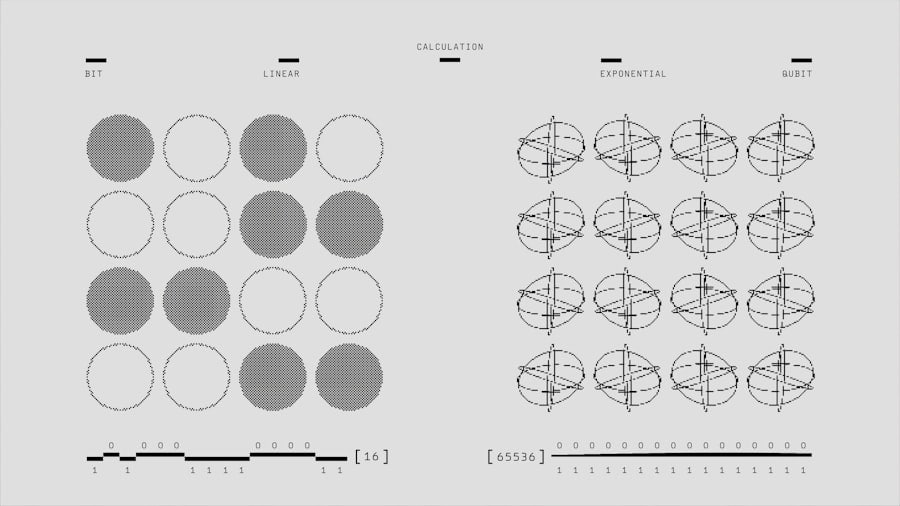
Geometric deep learning has shown great promise in leveraging graph and network data for various applications such as social network analysis, recommendation systems, and biological network modeling. Traditional machine learning methods struggle to effectively process graph-structured data due to its non-Euclidean nature. Geometric deep learning addresses this limitation by developing algorithms that can effectively capture and leverage the intrinsic geometric properties of graph and network data.
One of the key applications of geometric deep learning for graph and network data is social network analysis. By representing social networks as graphs or networks, geometric deep learning algorithms can capture the inherent relationships between individuals or entities, leading to more accurate and robust social network analysis models. Additionally, geometric deep learning has been used for tasks such as recommendation systems and biological network modeling, where the input data has a non-Euclidean structure.
Overall, leveraging geometric deep learning for graph and network data enables the development of algorithms capable of effectively processing and analyzing non-Euclidean data, leading to superior performance in tasks such as social network analysis, recommendation systems, and biological network modeling.
Geometric Deep Learning in Natural Language Processing and Speech Recognition
Geometric deep learning has significant potential in natural language processing (NLP) and speech recognition by enabling the development of algorithms capable of effectively processing and analyzing non-Euclidean language data represented as graphs or networks. Traditional NLP methods struggle to capture the inherent relationships between words or phrases due to their non-Euclidean nature. Geometric deep learning addresses this limitation by developing algorithms that can effectively capture and leverage the intrinsic geometric properties of language data.
One of the key applications of geometric deep learning in NLP is semantic parsing. By representing language as a structured graph or network, geometric deep learning algorithms can capture the inherent relationships between words or phrases, leading to more accurate and robust semantic parsing models. Additionally, geometric deep learning has been used for tasks such as sentiment analysis and speech recognition, where the input language data has a non-Euclidean structure.
Overall, leveraging geometric deep learning in NLP and speech recognition enables the development of algorithms capable of effectively processing and analyzing non-Euclidean language data, leading to superior performance in tasks such as semantic parsing, sentiment analysis, and speech recognition. In conclusion, geometric deep learning represents an exciting frontier in machine learning with diverse applications across various domains such as computer vision, robotics, graph analysis, NLP, and speech recognition. While it presents unique challenges related to handling non-Euclidean data and model interpretability, its potential for revolutionizing how we process complex data structures cannot be understated.
As research continues to advance in this field, we can expect to see even more innovative applications emerge along with solutions to current challenges. Geometric deep learning is poised to play a pivotal role in shaping the future of AI by enabling more effective processing and analysis of non-Euclidean data across a wide range of applications.
If you’re interested in the intersection of technology and virtual worlds, you may want to check out this article on metaverse platforms and ecosystems. It explores the social and virtual aspects of metaverse platforms and how they are shaping the future of digital interactions. Geometric deep learning could potentially play a role in enhancing the immersive experiences within these virtual worlds.
FAQs
What is geometric deep learning?
Geometric deep learning is a subfield of machine learning that focuses on developing algorithms and models capable of learning from and processing data with a geometric structure, such as graphs, point clouds, and manifolds.
What are the applications of geometric deep learning?
Geometric deep learning has applications in various fields, including computer vision, 3D object recognition, molecular chemistry, social network analysis, and recommendation systems.
What are some key challenges in geometric deep learning?
Some key challenges in geometric deep learning include developing models that can effectively handle irregular and unstructured data, designing algorithms that can capture and process geometric relationships, and scaling up to handle large-scale geometric datasets.
What are some popular geometric deep learning techniques?
Popular geometric deep learning techniques include graph neural networks (GNNs), convolutional neural networks (CNNs) for 3D data, point cloud processing methods, and manifold learning algorithms.
How is geometric deep learning different from traditional deep learning?
Geometric deep learning differs from traditional deep learning in that it focuses on learning and processing data with a geometric structure, such as graphs and manifolds, whereas traditional deep learning typically deals with grid-like data, such as images and sequences.










Leave a Reply